This is going to be a bit different than my other posts.
A few weeks ago, I stumbled across a video about the Collatz Conjecture. It was from one of the YouTube channels I follow, TippingPointMath. The video very clearly explains the Conjecture and gives a little background on the history of the problem.
Out of pure curiosity I began to play with the (as I now knew it) “3N+1 Conjecture” myself. I did not look much into other people’s methods of solving (though I did a quick search to ensure it was still an “unproven” conjecture), but attacked it myself from two specific angles.
The first attack was to evaluate what, in my mind, was a similar proposal, but one that is much easier to prove and observe. I looked at the “N+1 Conjecture”. That is, I formulated an algorithm similar to Collatz’s that goes:
{ N is a positive, whole integer
If N is even, N’=N/2; if N is odd, N’=N+1.}
I did not write out a formal proof, but I think it is easy to see that this algorithm always collapses to N=1, and then perpetuates a cycle of {1,2}. If you start out with an even N, N’ is obviously less than N; If N is odd, N’ will be greater than N by a value of 1, but this guarantees that N’ will be even, so then N”=N’/2=(N+1)/2. It is easy to see that N” will be less than N for all integers N>2.
A few examples of number chains this algorithm would produce:
Starting with N=64: {64,32,16,8,4,2,1,2,1…}
Starting with N=99: {99,100,50,25,26,13,14,7,8,4,2,1,2,1…}
Starting with N=214527: {214527, 214528, 107264, 53632, 26816, 13408, 6704, 3352, 1676, 838, 419, 420, 210, 105, 106, 53, 54, 27, 28, 14, 7, 8, 4, 2, 1, 2, 1…}
Even starting with obscure primes and odd numbers, it is easy to see the decline of the chains to the {1,2} cycle.
Another way to look at both the N+1 and the 3N+1 algorithms, is in reverse. In reverse the N+1 algorithm becomes:
{If N’ is odd, N=2*N’
If N’ is even, N=2*N’ AND N’-1}
By looking at them this way, a tree like structure emerges, where N’ can branch off into more than one Ns. For example, if N’ is 4, it could be that N is 8 and was divided by 2, or that N is 3 and 1 was added to N. Both situations will result in N’=4. This is best shown in plot format, where it clears displays a branching tree structure:
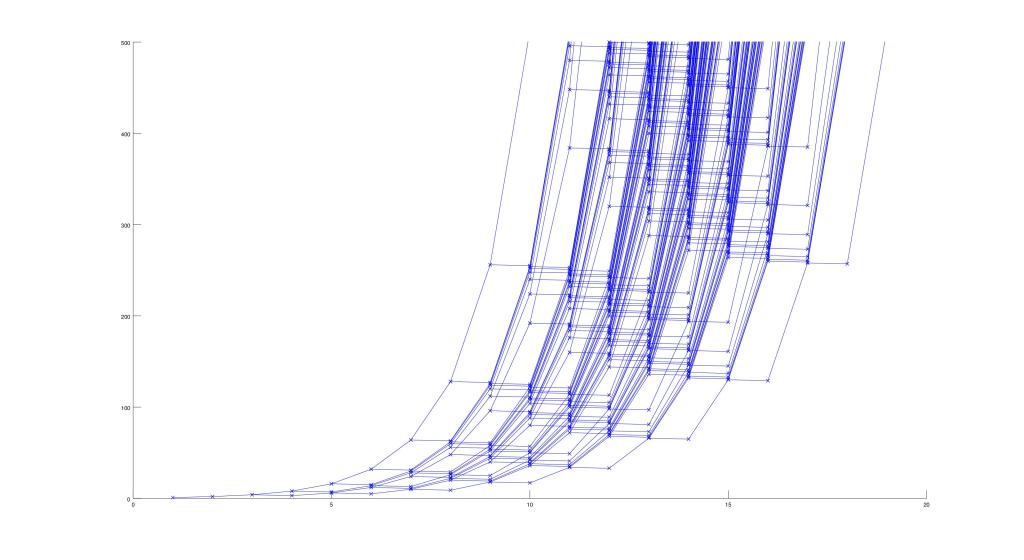
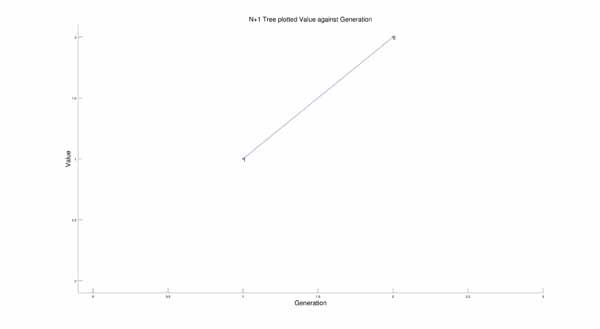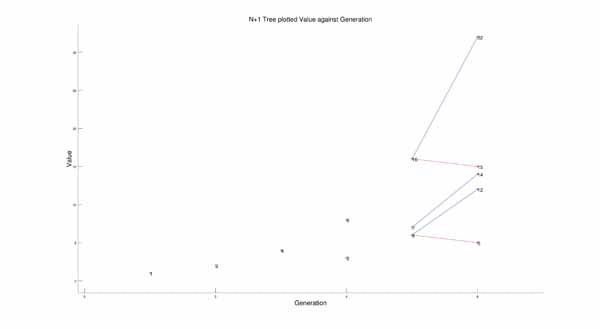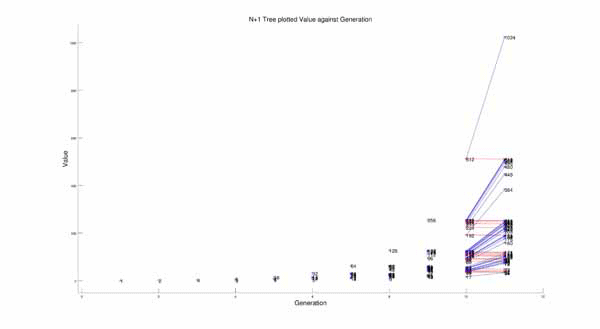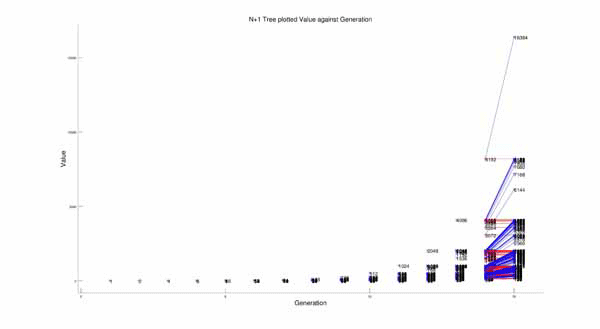
Though these plots show the tree structure, it does look very chaotic and as if there is no pattern to the way it all reduces to 1. After noticing a pattern in the “evenness” of the numbers in the chains I thought of an idea. I plotted the tree again, but on different axes. I plotted the points such that the value p of each number in the tree can be found by the equation:
p=x*2y
In order to still maintain the visualization of generations, I made it into a gif as well, with each step showing a separate generation.
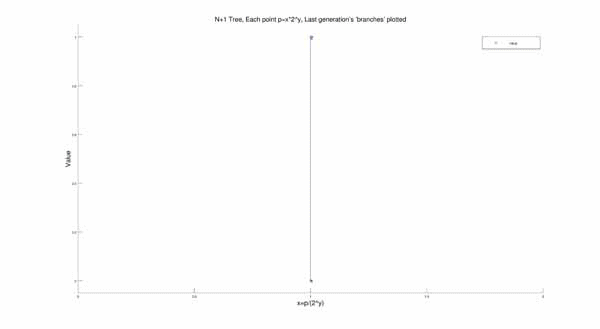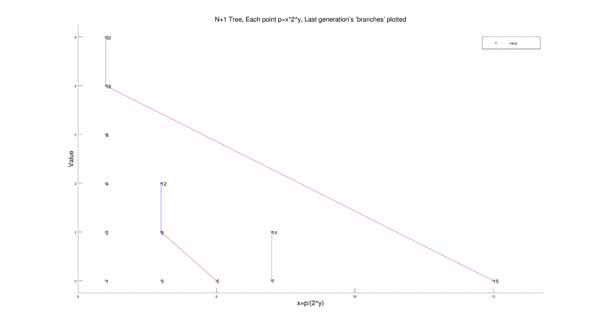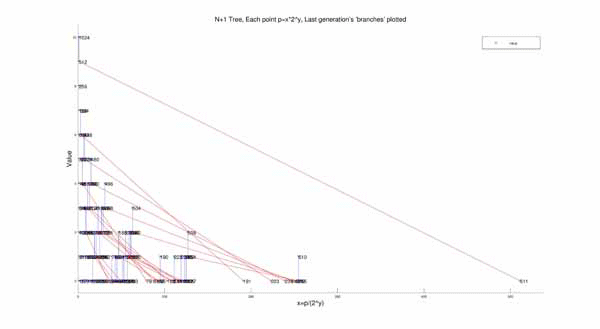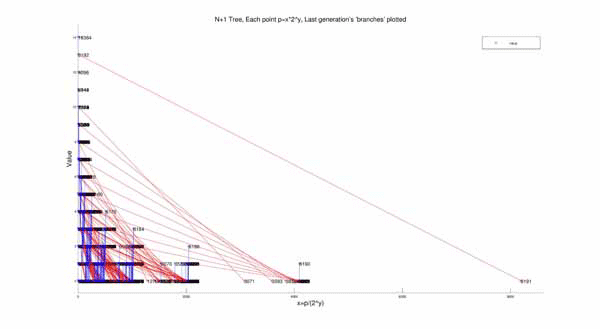
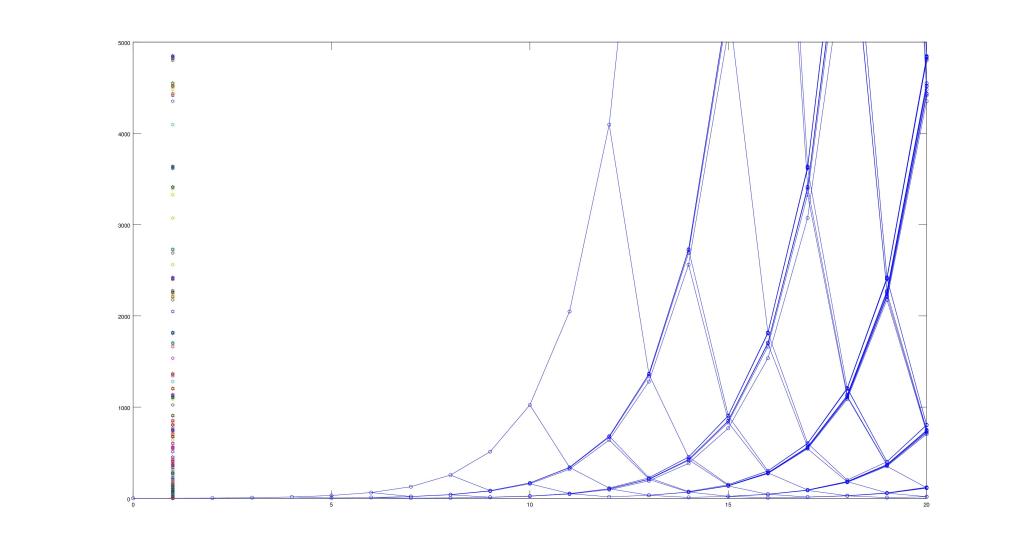
Then I made a few 20-generation plots to show how this structure looks on a grand scale:
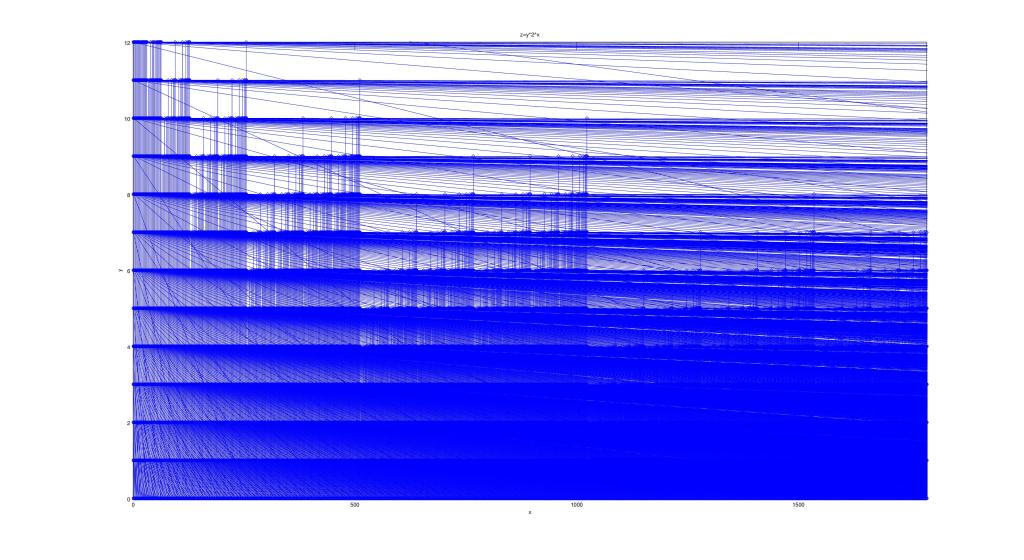
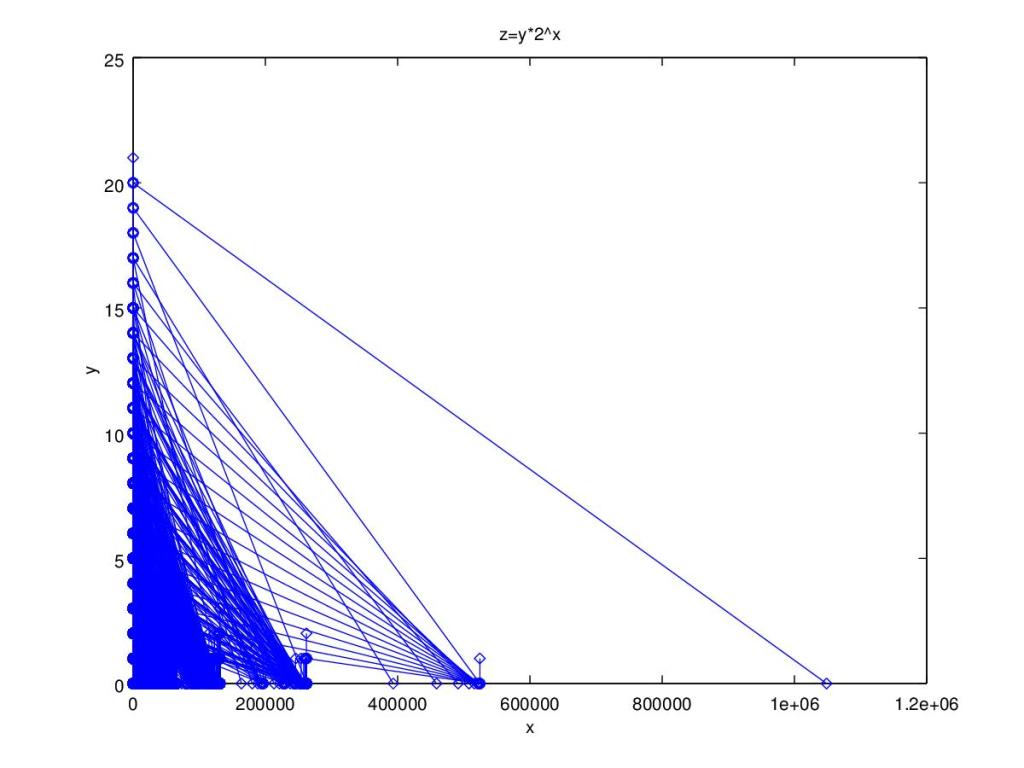

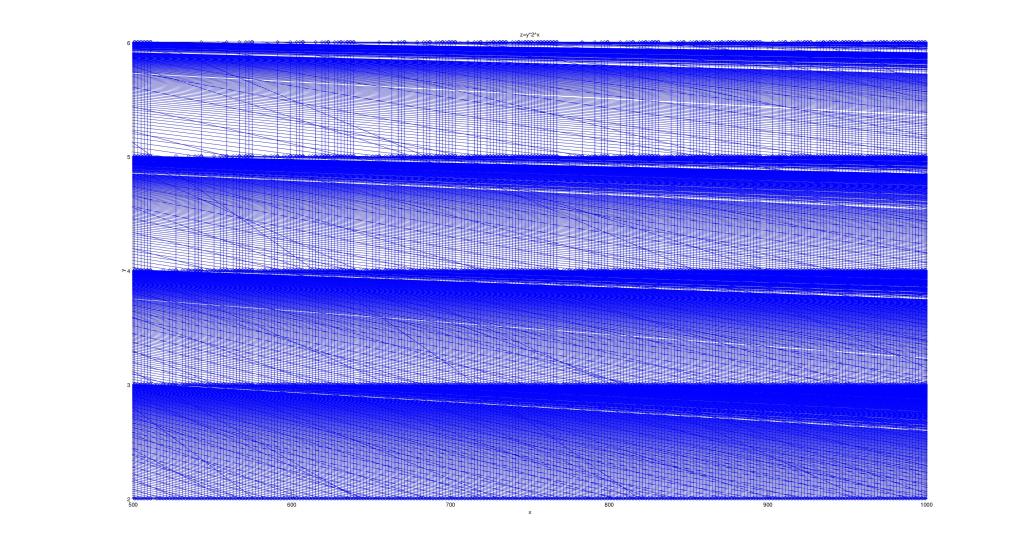
Now I began to attack the 3N+1 problem using similar techniques. First I figured out an algorithm that generates the reverse tree:
{If N’-1 is thirdable* and not even
N=1⁄3(N’-1) AND 2*N’
Otherwise,
N=2*N’ }
(*Sidenote: I use the word “thirdable” to describe the quality of a number to be divided by 3 evenly, with no remainder. Another way of saying this is that if a number is “thirdable” it has 3 as one of its factors)
From this I got a tree that looks like:
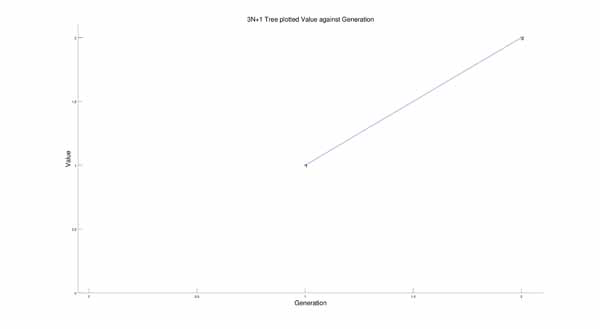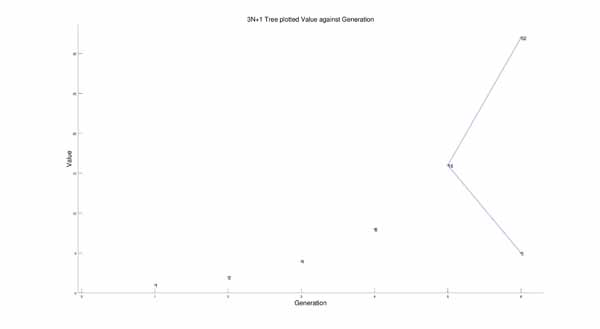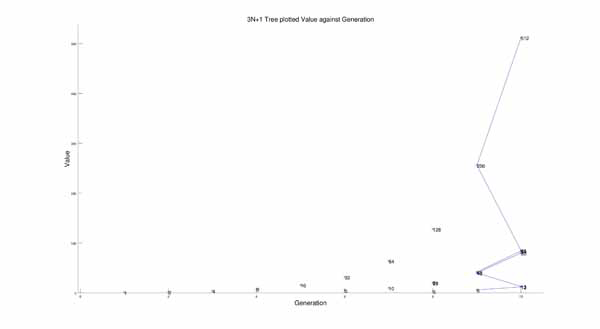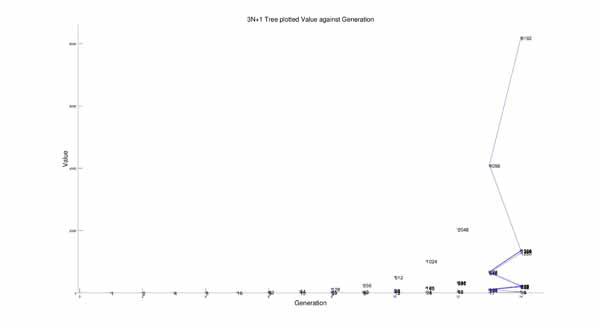
Again, you can see the branching tree-like organization, but it looks like chaos.
It did not do me any good to plot it on the same axes as I did for the N+1 algorithm, but after examining the ways the numbers branch off, I thought of a similar way to illustrate an analogous structure. I plotted the tree in a 3-Dimensional plot, such that the value of each point p can be given by the equation:
p=x*2y*3z
Again, I made a gif of how this tree “grows” such that each step shows the next generation of branches. This goes through 30 generations:
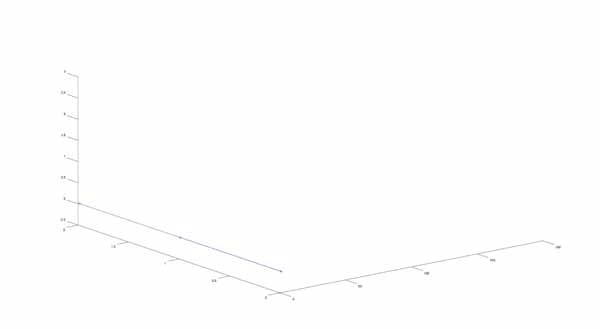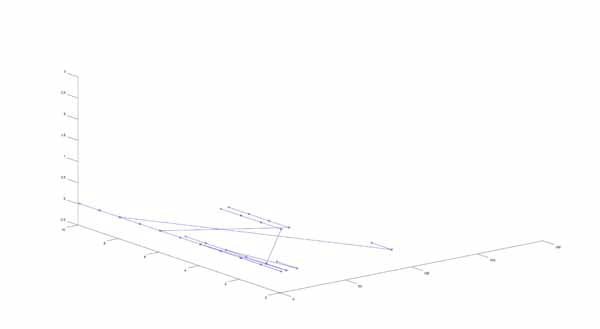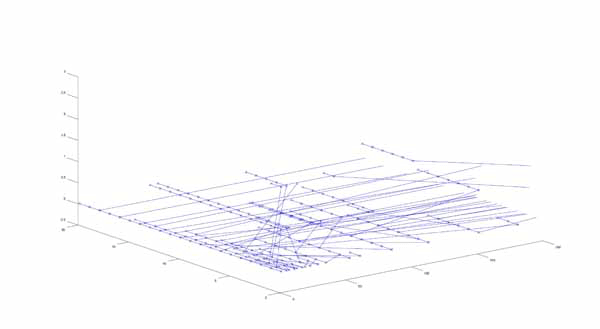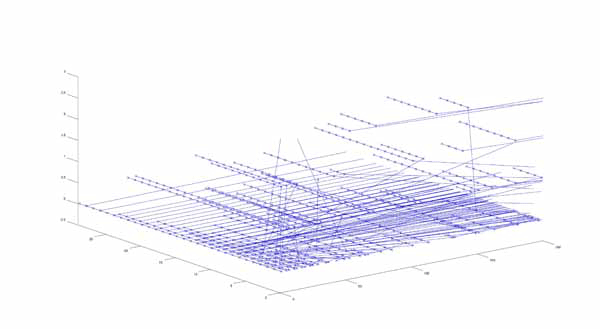
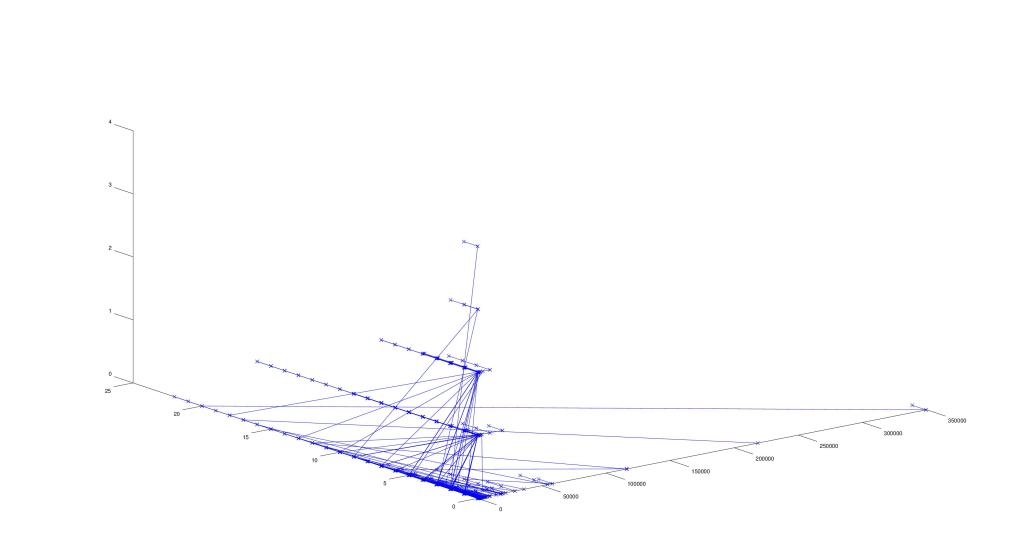
It was taking my computer a very long time to compute the higher generations so I wrote a different function which took N’ to be all integers less than a set value A. Here is a gif which inputs A to be various high values, the largest being N=10000.

And here is a zoomed out perspective with the largest N being 500:
Though the appearance of the branches growing has dissolved, it is my opinion that this is an illustration of structure. If this structure can be defined, it could lead to a proof of the Collatz Conjecture.
What do you all think, is there structure here? Am I on to something? I used Octave to create all of these plots, and then Photoshop to make them into gifs. If anyone is interested in seeing the functions I wrote to create them, please contact me.
Leave a reply to Stephanie Rivera Cancel reply